Tabla de contenido:
Video: ¿Cómo se hace la regresión lineal múltiple?
2024 Autor: Stanley Ellington | [email protected]. Última modificación: 2023-12-16 00:15
Comprender una relación en la que más de dos variables están presente, un regresión lineal múltiple se utiliza.
Ejemplo de uso de regresión lineal múltiple
- yI = variable dependiente: precio de XOM.
- Xi1 = tipos de interés.
- Xi2 = precio del petróleo.
- Xi3 = valor del índice S&P 500.
- Xi4= precio de los futuros del petróleo.
- B0 = intersección con el eje y en el tiempo cero.
Teniendo esto en cuenta, ¿cómo funciona la regresión lineal múltiple?
Regresión lineal múltiple intenta modelar la relación entre dos o más variables explicativas y una variable de respuesta ajustando un lineal ecuación a los datos observados. Cada valor de la variable independiente x está asociado con un valor de la variable dependiente y.
Además, ¿cuál es la ecuación para la regresión múltiple? Regresión múltiple . Regresión múltiple generalmente explica la relación entre múltiple variables independientes o predictoras y una variable dependiente o de criterio. los ecuación de regresión múltiple explicado anteriormente toma la siguiente forma: y = b1X1 + b2X2 +… + B X + c.
Además, ¿para qué se utiliza la regresión lineal múltiple?
Regresión múltiple es una extensión de simple regresión lineal . Está usado cuando queremos predecir el valor de una variable en función del valor de otras dos o más variables. La variable que queremos predecir se llama variable dependiente (o, a veces, variable de resultado, objetivo o criterio).
¿Cómo se hace la regresión lineal múltiple en Python?
Regresión lineal múltiple en Python
- Paso 1: Cargue el conjunto de datos de Boston.
- Paso 2: Configure las variables dependientes e independientes.
- Paso 3: Eche un vistazo a la variable independiente.
- Paso 4: Eche un vistazo a la variable dependiente.
- Paso 5: Divida los datos en conjuntos de prueba y de tren:
Recomendado:
¿Qué es Python de regresión lineal?
Regresión lineal (implementación de Python) La regresión lineal es un enfoque estadístico para modelar la relación entre una variable dependiente con un conjunto dado de variables independientes. Nota: En este artículo, nos referimos a las variables dependientes como respuesta y las variables independientes como características para simplificar
¿Qué es la regresión lineal de los datos?
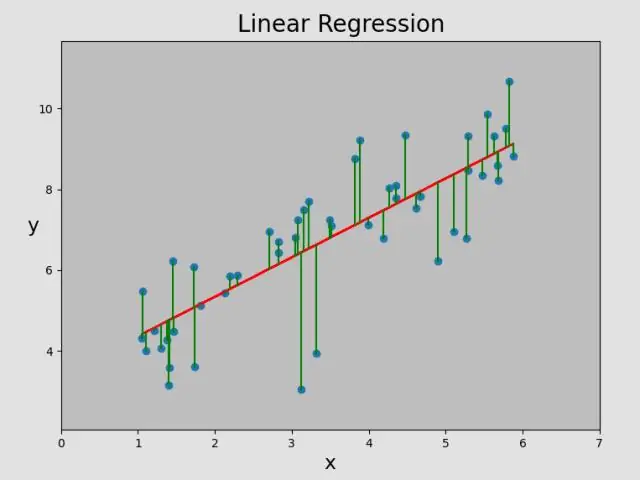
La regresión lineal intenta modelar la relación entre dos variables ajustando una ecuación lineal a los datos observados. Una línea de regresión lineal tiene una ecuación de la forma Y = a + bX, donde X es la variable explicativa e Y es la variable dependiente
¿Cómo elige el mejor modelo de regresión múltiple?
Al elegir un modelo lineal, estos son factores a tener en cuenta: Solo compare modelos lineales para el mismo conjunto de datos. Encuentre un modelo con un R2 ajustado alto. Asegúrese de que este modelo tenga residuos distribuidos equitativamente alrededor de cero. Asegúrese de que los errores de este modelo estén dentro de un ancho de banda pequeño
¿Qué es la regresión lineal múltiple en R?
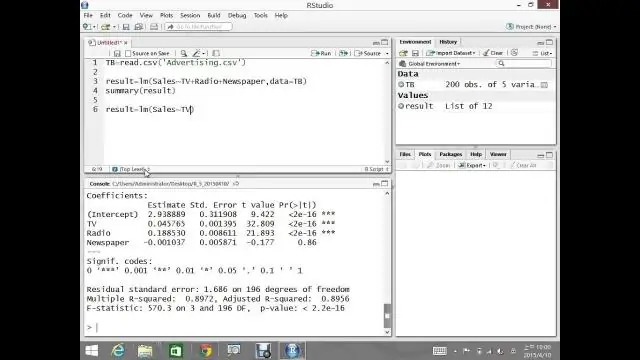
La regresión lineal múltiple es una extensión de la regresión lineal simple utilizada para predecir una variable de resultado (y) sobre la base de múltiples variables predictoras distintas (x). Miden la asociación entre la variable predictora y el resultado
¿Qué suposiciones hace el algoritmo de aprendizaje automático de regresión lineal?
Supuestos sobre los estimadores: Las variables independientes se miden sin error. Las variables independientes son linealmente independientes entre sí, es decir, no hay multicolinealidad en los datos