Video: ¿Cuál es la fórmula de Euler usando el número de caras del tetraedro que tienen vértices como 4 y 6 aristas?
2024 Autor: Stanley Ellington | [email protected]. Última modificación: 2023-12-16 00:15
Esta página enumera las pruebas de la Fórmula de Euler : por cualquier poliedro convexo, el número de vértices y caras juntos son exactamente dos más que el número de bordes . Simbólicamente V − E + F = 2. Para ejemplo, un tetraedro tiene cuatro vértices , cuatro caras y seis bordes ; 4 - 6 + 4 =2.
En consecuencia, ¿cuál será el número de caras si hay 6 vértices y 12 aristas?
Un cubo o un cuboide es una forma tridimensional que tiene 12 aristas , 8 esquinas o vértices , y 6 caras.
También se puede preguntar, ¿cómo funciona la fórmula de Euler? Fórmula de Euler , Cualquiera de los dos importantes teoremas matemáticos de Leonhard Euler . La primera es una invariancia topológica (ver topología) que relaciona el número de caras, vértices y aristas de cualquier poliedro. Se escribe F + V = E + 2, donde F es el número de caras, V el número de vértices y E el número de aristas.
¿Cuál es la fórmula para la relación entre el número de caras, vértices y aristas de un cubo?
V - E + F = 2; o, en palabras: el número de vértices , menos el número de bordes , más el número de caras , es igual para dos.
¿Cuál es la fórmula del poliedro de Euler?
Este teorema implica Fórmula poliédrica de Euler (aveces llamado Fórmula de Euler ). Hoy diríamos este resultado como: El número de vértices V, caras F y aristas E en una estructura tridimensional convexa. poliedro , satisface V + F - E = 2.
Recomendado:
¿Es el número de serie el mismo que el número de VIN en una casa móvil?
1) Hay una etiqueta de papel en el interior de todas las casas móviles fabricadas desde junio de 1976, llamada "placa de datos", que enumera el número de VIN (también llamado número de serie), junto con otros datos sobre la fabricación de la casa. . El VIN se denominará el número de serie del fabricante en la placa de datos
¿Qué tan caras son las tejas solares?
El precio promedio de instalación del techo para un techo de tejas solares cuesta entre $ 60,000 y $ 75,000 dependiendo de la pendiente, la inclinación y el tamaño de su techo. Puede esperar pagar de $ 21 a $ 25 por pie cuadrado o de $ 2,100 a $ 2,500 por cuadrado instalado en una casa de un solo piso de tamaño estándar
¿Cómo encuentra el costo unitario del producto usando el costeo tradicional?
Sume sus costos totales directos de materiales, sus costos totales de mano de obra directa y sus costos indirectos totales de fabricación en los que incurrió durante el período para determinar los costos totales del producto. Divida su resultado por la cantidad de productos que fabricó durante el período para determinar el costo de su producto por unidad
¿Cómo se multiplica un número mixto por un número entero?
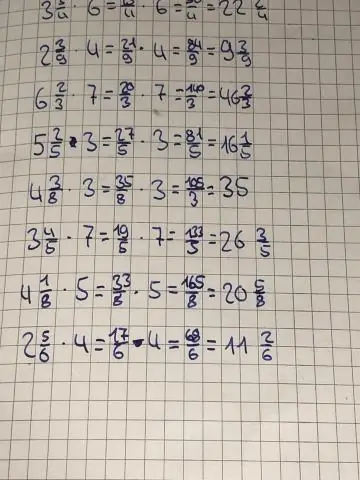
Multiplicación de un número mixto y un número entero El número mixto se convierte en una fracción impropia y el número entero se escribe como una fracción con denominador. Se lleva a cabo la multiplicación de las fracciones y, si es necesario, se simplifica. La fracción resultante se escribe como un número mixto en la forma más simple
¿Cuál es el costo de los bienes vendidos usando el método FIFO?
Con este método, las empresas suman el costo total de los bienes comprados o producidos durante un tiempo específico. Luego, esta cantidad se divide por la cantidad de artículos que la empresa compró o produjo durante ese mismo período. Esto le da a la empresa un costo promedio por artículo