
Tabla de contenido:
- Autor Stanley Ellington [email protected].
- Public 2023-12-16 00:15.
- Última modificación 2025-01-22 15:57.
En cálculo diferencial, un punto de inflexión , punto de inflexión , flexión o inflexión (Inglés británico: inflexión ) es un punto en una curva plana continua en la que la curva cambia de cóncava (cóncava hacia abajo) a convexa (cóncava hacia arriba), o viceversa.
También sepa, ¿cómo encuentra el punto de inflexión?
Resumen
- Un punto de inflexión es un punto en la gráfica de una función en el que cambia la concavidad.
- Los puntos de inflexión pueden ocurrir donde la segunda derivada es cero. En otras palabras, resuelva f '' = 0 para encontrar los puntos de inflexión potenciales.
- Incluso si f '' (c) = 0, no se puede concluir que haya una inflexión en x = c.
En segundo lugar, ¿cuántos puntos son inflexión? Puntos de inflexión son donde la función cambia de concavidad. La segunda derivada debe ser igual a cero cuando la función cambia de concavidad. Pero debemos comprobar puntos a cada lado para asegurarse de que la concavidad realmente cambie. Entonces, x = 15√21 es posible punto de inflexión.
Considerando esto, ¿qué significa no tener punto de inflexión?
Explicación: A punto de inflexión es un punto en el gráfico en el que cambia la concavidad del gráfico. Si una función no está definida en algún valor de x, hay pueden ser sin punto de inflexión . Sin embargo, la concavidad pueden cambian a medida que pasamos, de izquierda a derecha a través de valores de x para los que la función no está definida.
¿Los puntos de inflexión tienen que estar en el dominio?
Si una función cambia de cóncava hacia arriba a cóncava hacia abajo o viceversa alrededor de una punto , se llama punto de inflexión de la función. Al determinar los intervalos donde una función es cóncava hacia arriba o cóncava hacia abajo, primero encuentra dominio valores donde f ″ (x) = 0 o f ″ (x) lo hace no existe.
Recomendado:
¿Cuál es el punto de fusión y ebullición de la naftaleno?
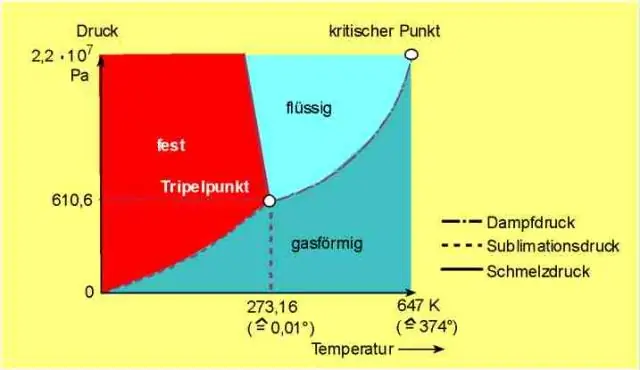
El ingrediente que se encuentra en las bolas de polilla es naftalina, o naftalina, alquitrán de alcanfor y alquitrán blanco. Se elabora mediante cristalización a partir de alquitrán de hulla. Es un sólido blanco con un olor muy fuerte. Su punto de fusión es de 80,2 grados C y su punto de ebullición es de 217,9 grados C
¿Cuál de las siguientes batallas se considera el punto de inflexión en el cuestionario sobre la guerra en Europa?

La batalla de Stalingrado detuvo el avance alemán en la Segunda Guerra Mundial y marcó el punto de inflexión de la guerra en Europa del Este
¿Cuál fue el punto de inflexión en la Segunda Guerra Mundial?

Hace 70 años, diciembre de 1941: Punto de inflexión de la Segunda Guerra Mundial. La batalla de Stalingrado es considerada por los historiadores como un punto de inflexión decisivo de la Segunda Guerra Mundial, durante la cual las fuerzas alemanas fueron derrotadas después de cinco meses de combate
¿Cuál es la diferencia entre las matemáticas de interés simple y compuesto?
Con interés simple, la cantidad de interés se fija durante un período de tiempo. Es importante tener en cuenta que, con un interés simple, la cantidad ganada seguirá siendo la misma todos los años. Interés compuesto. El interés compuesto es el tipo de interés que los bancos pagan con mayor frecuencia a los ahorradores
¿Cuál es la definición de director en matemáticas?

Principal. más La cantidad total de dinero prestado (o invertido), sin incluir intereses ni dividendos. Ejemplo: Alex pide prestados $ 1,000 del banco. El capital del préstamo es de $ 1,000
